In a preview post, I have written about my 3d engine and skeleton animation. My goal was to export an animation from Blender (2.49) and play it back into an another program. This is achieved now and works correctly.
But I have met problems because I misunderstood the different coordinate spaces involved and how they are related to each other in Blender. When you understand those coordinate spaces, a big part of the game consist of using the good maths to build back the animation.
Let's explore the blender skeletal animation system with a special focus on the different coordinate spaces. When you know/understand the needed informations, you can export them by using the Blender Python API.
Armature
An armature is a hierarchal set of bones. One bone can have several children. One bone has none or one parent. The picture below shows two bones. The top one and the bottom one are respectively the child and the parent . This is indicated by the dashed line.
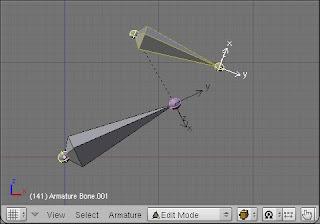
A bone can be
connected or not to its parent.
Connected means that the child's head is at the same position of the parent's tail, and it will remains as this while editing. This feature is useful while editing the armature for structure as arms or spine. But as we are not interested in editing but playing back the animation, this information is not important.
Bone anatomy
The picture below shows one bone in edit mode. A bone is composed of two points, the head and the tail, represented by the spheres, respectively at the bottom and the top of the bone. There are other parameters that characterize a bone, but I would like to focus on those.

In Blender, when you had an armature into a 3d scene (Shift A, Add > Armature), you obtain one bone of one unit length pointing in the world z-axis, as in the picture above. So far, problems arise, and it is about he bone axis... thus the bone space.
The bone space
When you enable bone axis drawing in the Armature tab from the editing panel (F9), you notice that the bone axis (in white) are not align with the world axis (red, blue, and green). And that is very disturbing at first sight because of this counter-intuitive aspect.
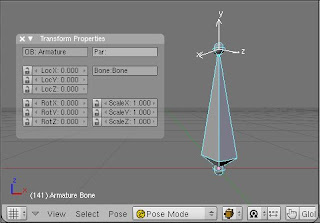
The picture above shows the same bone but in pose mode. By looking the transform properties floating panel you notice that the bone has not been rotated (RotX/Y/Z is 0). Hmmm, so, why the bone axis are not aligned with the world axis? Because bone are really typical object in Blender. They are different from other objects such as mesh, camera, or light, about how local axis is defined.
When you edit an armature, you are basically defining bones hierarchy and placing points as bone heads and bone tails. As a bone is defined by two points, you can not tell how a bone is rotated. Until a convention is defined.
The convention used in blender is as followed:
- The Y axis is aligned along the bone length, that is the normalized vector formed by the head and tail points.
- The X and Z axis has the same coordinates as Y, but rotated. That is X=(Yy, Yz, Yx), Z=(Yz, Yx, Yy).
- A rotation angle around the Y axis is defined. Called "Roll" in the properties panel in edit mode.
X, Y, Z formed the
bone space. Which is important for the animation because as you will see in the next chapter, the transformations are expressed in that space.
For this purpose, the essential information about the structure of the armature are, for each bone:
- its name
- the name of its parent (if it has one)
- its transform matrix in armature space
- its rotation matrix in bone space
Animation curves
The picture below is a screen-shot of the Ipo Curve Editor displaying pose curves of one bone. This is visible by selecting "Pose" from the "Ipo Type" combo-box. Here again, you can see that bones are very specific.

Compared with Object Ipo Curves, Bone Ipo Curves are very basic. The ten curves concern "only" the three transformations: translation (LocX, LocY, LocZ), rotation (QuatW, QuatX, QuatY, QuatZ), and scaling (ScaleX, ScaleY, ScaleZ). Notice that quarternion are used for rotation, that's why the x,y,z values vary between 0 and 1, and w between -1 and 1.
One important point to note down for later : those transformations are expressed in bone space.
The skin
The aim of skeletal animation is to deform a skin by moving bones. The skin is often a mesh which is a bunch of connected vertices forming edges and faces. When a bone moves, it also moves the vertices associated to it, thus the skin.
In Blender, bones and vertex groups are associated when they have the same name.

The picture above illustrates the association of a skin and a skeleton. On the left the Outliner Window shows two Vertex Groups named "bottom" and "top", the latter is selected. One the right the 3D Window, in Weight Paint mode, shows the Vertex Groups "bottom" and "top" respectively in blue and red. The armature with the bone names are displayed.
The vertex coordinates of the mesh are expressed in the
object space.
The animation: the all together
We have seen all the elements involved in skeletal animation. Let's resume all the informations we can retrieve by the Blender Python API.
- The skin: the vertex coordinates in object space
- The skeleton: the bones hierarchy and transform matrices in armature space and in bone space
- The bone animation curves in bone space
- The vertexgroups
The skin and the skeleton is either in bind pose or current pose (see this presentation for explanation of those poses). The armature and the mesh are exported in bind pose. The goal is to compute the vertex positions of the mesh in current pose.
Let v the position of a vertex in bind pose in object space and v' its position in current pose. We know v and we have to compute v'.
As the animation curves are expressed in bone space, we need the vertex position from object space v in that space. This is done by multiplying the vertex position in object space v by the inverse of transform matrix in armature space B of the bone b associated with the vertex.
v_bonespace = inv(B_b)v
Then, we multiply this by the transform matrix P_b computed from the animation curves of the bone b. We obtain v' in bone space.
v'_bonespace = P_bv_bonespace
What is left now, is to compute back that position in the armature space. For this we multiply it by the matrix product of rotation and translation of each bone in current pose, from the bone of interest to the root bone. That's it =).









